Optical Tweezers
Project 1 - Investigation on rheological properties of amphiphilic block copolymers
Project 3 - Blue algae transgenic engineering
Project 4 - Protein Engineering
Introduction to Optical Tweezers
About the research
Our lab, the Laser Biology Lab of USTC, is established based on the technology of optical tweezers. When optical tweezers were first invented in 1986, Prof Li Yinmei from USTC got known of this technology and introduced it into China and began research biological issues with optical tweezers for the first time in 1989. Later after several years mastering this technology, she was able to write a book on optical tweezers in 1996, which was the first book in China to introduce this technology systematically to common readers. Till now, our lab has complete system and devices on optical tweezers, and has not only done a lot of research on optical tweezers itself, but also has solved many biological and medical problems by using this tool. Because our lab relies on the Physics Department in my university, and there is no biophysics specialty in my campus, our lab lacks enough researchers whose backgrounds are biology. Therefore, along so many years, although a lot of medical and biological institutes have cooperated with us on problems such as cell merging and chromosome sorting, we still have little knowledge in biology itself. Optical tweezers, in some sense, is a technological tool to solve others’ problems, rather than solve our problems. So it is a problem for our lab to overcome – to build a strong biology background and guide our own research on biology.
Besides biology, optical tweezers is also a useful tool in physics and chemistry experiment. For example, we use optical tweezers to investigate properties of glues and other soft condensed matters. Other applications can be found in surface physics. We have successfully applied optical tweezers in the research of disperse system since 2000. Because of the wide range usages of optical tweezers, and our strong basis in physics, we actually use optical tweezers with a emphasize more on physics problems than biology problems.
Project 1 - Investigation on rheological properties of amphiphilic block copolymers by optical tweezers
Amphiphilic block copolymers have a wide application in drug delivery and in dealing with effluents. One of the amphiphilic block copolymers, PEO-PPO-PEP is a material with viscoelasticity, its reaction to interference is relevant to its frequency, which amounts to several thousand Hz and not available to evaluate by current commercial equipment.
Our experiment is able to detect the frequency with a level of 10000 Hz according to the theory of Brownian movement with the help of optical tweezers. We aim to measure modulus of elasticity G’ and loss modulus G’’, establish a new method to measure the above parameters and its relevance with time factor with the help of optical tweezers, and to find the principle of glues’ aging. The methods established by the experiment would have a versatile suitability to the research of all amphiphilic block copolymers.
Semiflexible polymers are of great biological importance in determining the mechanical properties of cells. Techniques collectively known as microrheology have recently been developed to measure the viscoelastic properties of solutions of submicroliter volumes. Our research is also within such aims. Detail techniques about microrheology can be found here -
Karim M. Addas, C. F. S., 3 and Jay X. Tang1,2 (2004). "Microrheology of solutions of semiflexible biopolymer filaments using laser tweezers interferometry." PHYSICAL REVIEW E 70(021503).
G Pesce1, A. C. D. L., G Rusciano1, P A Netti2,3, S Fusco2,3 and and A. Sasso1 (2009). "Microrheology of complex fluids using optical tweezers: a comparison with macrorheological measurements." JOURNAL OF OPTICS A 11(034016).
Larson R.G. The structure and rheology of complex fluids (Oxford 1999)(ISBN 019512197X).
Experiment Record
01/03/2010 Kramers-Kronig Integration by Maple 13
I use Maple to obtain the analytical solution of the Kramers-Kronig relation, which is key to solve the imaginary part of the compliance alpha. Kramers-Kronig relation is widely used to obtain solution for the imaginary part or real part of a complex variable if its counterpart is known. In this case, I want to solve the compliance alpha, which is a complex variable in the complex fluid mechanics, saying, alpha* = alpha' + i alpha''. The compliance alpha has a reciprocal relationship with the intended complex modulus through the General Einstein-Stokes relation and the strain-stress relation. Thus I can obtain the intended G modulus. Though it is impossible to obtain an analytical solution for real experiment, but the analytical solution on very special values designated can gain me a basic review of the picture, mainly the relationship between modulus and frequency, and the configuration of power spectral density and mean squared density. Later I also employed both Maple 13 and Mathematic 7 to obtain the numerical solution in the continuous domain, which is proved unsuccessful with very low convergent ending. This, later help me determine my mind in using Matlab to gain a solution by using discrete numerical method.
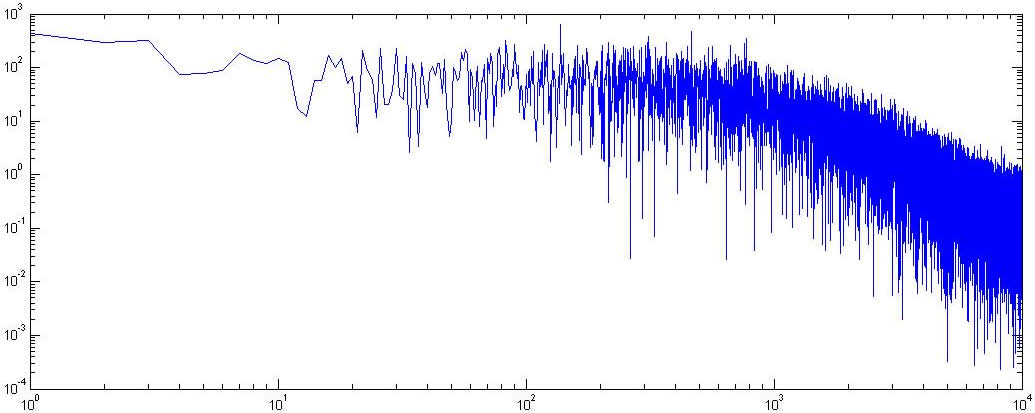
03/19/2010 Power Spectrum Density (PSD) calculation with Mean Square Displacement (MSD) data by Origin 8
By using photodiode devices (four quadrant detector) we obtained MSD information of a sphere in the flow exerted by piezoelectricity platform. The MSD can be conveniently transformed to its frequency domain, PSD, which we will use in the numerical integration of Kramers-Kronig relation. We first measured groups of MSD data, which we will use for a statistical average. The calculation is easy done both on Origin and Matlab.
MSD data (1 group of 10 groups)

PSD Figure (1 group with no statistical averaging)
03/22/2010 Kramers-Kronig Integration by Discrete Cosine Transformation and Discrete Sine Transformation by MATLAB 7.8
I use method indicated in the material below, to transform the Kramers-Kronig Integration to a double variable integration - a sine transformation and a cosine transformation, which is conveniently done on the cases here.
B. Schnurr, F. Gittes, F. C. MacKintosh, and C. F. Schmidt, Determining Microscopic Viscoelasticity in Flexible and Semiflexible Polymer Networks from Thermal Fluctuations, Macromolecules 1997, 30, 7781-7792
Champeney, D. C, Fourier Transforms and Their Physical Applications. New York: Academic Press 1973
To be continued
Project 2 - Direct measurements of constrained Brownian motion of an isolated sphere approaching another sphere
In fluid mechanics and Biophysics, the surface phenomena is an important issue which contains interesting physics. What's the diffusion coefficient of a sphere when it approaches the surface (eg, glass), and will the motion be any different from normal state when a cell polymer approaches the membrane? While the surface phenomena is basically understood by scientists, the sphere-sphere interaction cannot be ignored and there have been several reports on that. We can never ignore the sphere-sphere interactions because hundreds of thousands of them distributed in the fluid, and one of the reasons why current theoretical estimation does not meet well with the experiment value comes from the ignorance of sphere-sphere interaction. The report below, demonstrates that the Brownian motion of isolated spheres is underestimated with only surface interaction considered.
[1] Binhua Lin, Jonathan Yu, and Stuart A. Rice, Direct measurements of constrained Brownian motion of an isolated sphere between two walls, PHYSICAL REVIEW E, VOLUME 62, NUMBER 3
While reports have been made on the sphere-sphere interaction, most of them only calculates in the situation where the interacting spheres are of the same size [3]. We would like to have an investigation of the sphere-sphere interaction, but with unequal colloid sizes.. We use double-optical tweezers method, first fix two spheres by two optical traps at a distance, then measure the MSD information of one sphere. Change the distance, and again measure the MSD info. In this way we obtain the MSD-distance diagram. The MSD info can be used to calculate the diffusion coefficient by the method below -
[2] Branimir Lukić, Sylvia Jeney, Željko Sviben, Andrzej J. Kulik, Ernst-Ludwig Florin, and László Forró, Motion of a colloidal particle in an optical trap, PHYSICAL REVIEW E 76, 011112 (2007)
[3] Crocker, J. C. (1997). "Measurement of the hydrodynamic corrections to the Brownian motion of two colloidal spheres." Journal of Chemical Physics 106(7): 2837-2840.
Experiment Record
03/19/2010 Double Optical Tweezers grabbing two spheres successfully
I use a He-Ne 633nm laser to trap a 1 micrometer sphere, and another laser with different wavelength (a semi-conductor laser of 800nm) to trap another sphere. The two beams are coupled in the same direction. As they are of different wavelength, no interference is observed and so they can capture spheres independently. The two beams, one is fixed by the piezoelectric platform, and the other can be adjusted by a piezoelectric rotating mirror. So the two spheres that are captured by different OT can be seperated at a designated length.
04/02/2010 Measurement of the diffusion coefficient of a single Brownian sphere (1 micrometer diameter)
I use a four-quadrant detector to measure the sphere's Brownian movement. Because the four-quadrant detector only gives me voltage signals, I have to transform it to displacement signals. The relationship can be written as x = beta * V, V stands for voltage. In order to get the value 'beta', I have to use some displacement sample (by using CCD signals) and divide them with voltage. Because the CCD signal is far less sensitive than the voltage signal, I have to exert a enough large shear flow on the sphere in order to get an obvious displacement. As soon as the coefficent 'beta' is eatabished, I can easily transform the voltage signal into displacement signal, even if the displacement is invisible by CCD (the case that the sphere is trapped by OT without shear flow, or a stationary sphere with limited Brownian movement under OT).
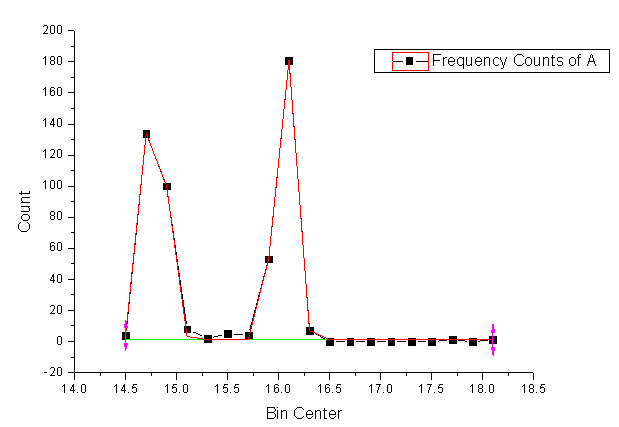
The above figure shows frequency Count for CCD signal (sphere with sine triangle wave shear flow), the two peaks stands for the two equilibrium states of moving sphere in OT. By dual-peak Gaussian simulation, we get the distance of the two equilibrium places.
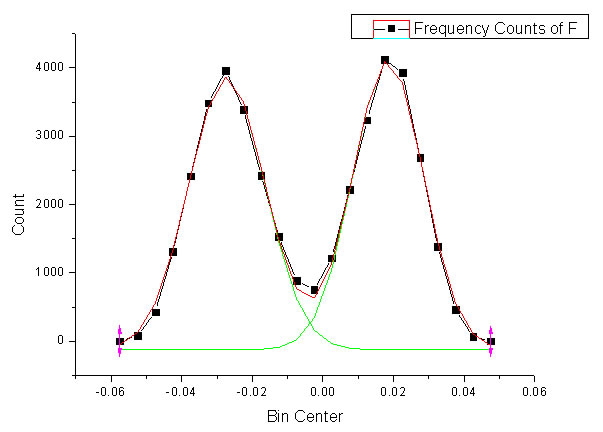
The above figure shows the voltage signal of the sphere movement stated above. Using the same strategy, we get the voltage distance of the two equilibrium status, and thus we can conclude the value of 'beta'.
Later I measure the voltage signal (from four-quadrant detector) of contrained Brownian sphere without applying flows. And transform it to displacement signal by multiplying 'beta'.
I use the displacement signal to calculate MSD, and use the fluctuation-dissipation theorem '< delta x^2> = 2 D t ' to calculate the diffusion coefficient D. Later I compare it with the theoretical value - Stokes-Einstein Relation - D = KT/ (6 pi n a) where n is the viscosity and a is the radius of sphere. The experimental value fits well to the theoretical value.

The above figure shows the MSD information. The latter part of the figure contains the influence of OT, and the linear part (first part) of the figure leads to free Brownian movement. I use the linear part to calculate the diffusion coefficient D, and compare it with the Stokes-Einstein Relation, and they fits well.
04/07/2010 Measurement of the diffusion coefficient of a single Brownian sphere (3 micrometer diameter)
Because my experiment is to measure the diffusion coefficient of a smalled sphere approaching a bigger one. So I measure 'D' of the bigger one first, using the previous approach. The experimental value fits well to the theoretical value.
To be continued
Project 3 - Blue algae transgenic engineering
Project 4 - Protein Engineering
Intro
Optical Tweezers are first invented by Arther Ashkin from Bell Lab in the 1980s. It comes from the principle of optical pressure. Because it gives a three-dimensional pressure on micro transparent particle when light focus on it, and we can move it when moving the focused laser. The many special properties of this optical tool create and broaden new ways to research behavior of single cell or its organ.
The system of optical tweezers:
 |
 |
|---|---|
| Single molecule nano operation | Composite system of Laser Scalpel and Optical Tweezers |
Laser is not absolutely direct, it has diverging angle. When laser penetrate through a transparent object, the different index of refraction forms a 3D gradient force. This force is somehow like a black hole to transparent objects. Thus we can use this force to attract and move objects around on our will.
 |
 |
|---|---|
| Gauss Laser | Laser trapping force |
 |
 |
| Operation Platform | Optical Path |
The following applications are few basic examples among those researches our lab have done before.

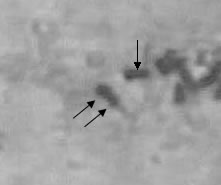 |
 |
|---|---|
| Chromosome | Chromosome Cut |
Many patients present a transformation in red blood cell(RBC), especially in its shape. Measure the modulus elasticity of RBC will add our understanding to some diseases. We use a polystyrene sphere to hold the cell, and optical tweezers to pull its other end. With the change of shape, we can calculate its elasticity.
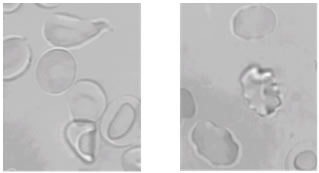 |
|---|
| Measuring elasticity of RBC |
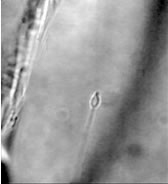 |
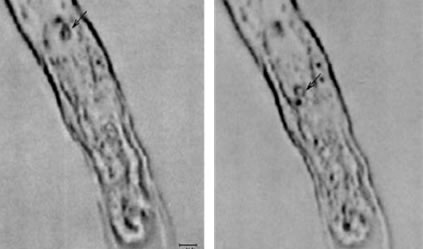 |
|---|---|
| Separate lively Sperm | Manipulate Cell Organ |
My research
As I stated above, our lab is initially based on the technology of optical tweezers. The main purpose of my entering the lab is also to study this technology. I initially apply to research in blue algae genetical engineering, in which optical tweezers are applied. I take the research as my college summer research project, an experimental course of which research plan is on one’s own choice. However, the blue algae research requires some extra effort (see Blue algae genetical engineering), which is not suitable for my summer college research project (which requires some definite results). So I turn to do laser ablation research instead during this summer (2009).
I understand the importance of optical tweezers and have learned its main principle, operation method and basic application in part time. I have taken the introductory experiment on optical tweezers, from which I learn how to grasp particles, how to calculate the light trapping force, and take a glimpse at the construction of its system. I have also repeated some of the basic applications listed above. A lot more has to be learned to get full acquainted with the technology. Now my mentor has distributed me a project (amphiphilic block copolymers research) involved with optical tweezers as my undergraduate dissertation, so I have the chance now to get a deeper understanding of its usages. And also, I hope to apply it to the genetical engineering of blue algae and protein folding in the remaining days if I have the chance.